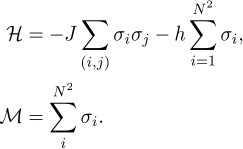
|
In this work, we approach the problem of estimation of macroscopic equillibrium properties of the 2D Ising model of ferromagnetic systems from a machine learning
perspective. This problem boils down to building supervised learning models of Hamiltonian and
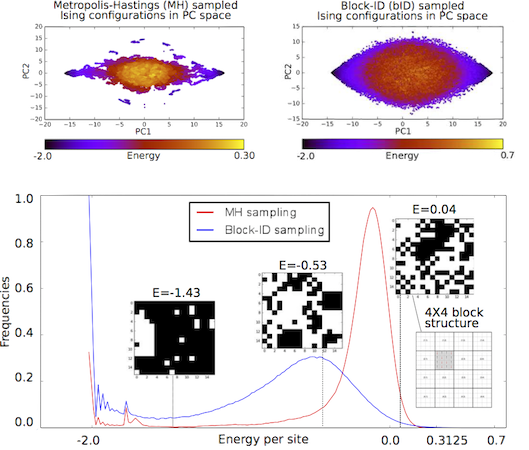
Magnetization operators defined by For the optimal performance of machine learning algorithms well-balanced representative datasets are needed, containing microstates in the energy range of the Ising system at equillibrium. We elucidate the shortcomings of the classical Metropolis Monte-Carlo methods for generation of such training datasets, specifically, imbalance between energy class representatives and poor within-class variability, and develop a new sampling technique called block-ID (bID). The bID method decomposes the 2D system of spins (viewed as a 2D image where spins directed up or down are shown as white or black pixels) into smaller square blocks with a dimension K no greater than 5 and samples two disjoint "half"-complete spaces of unique KxK Ising configurations categorized into energy classes to find a candidate block. A random walk that uniformly samples all energy levels of each subspace of KxK Ising systems, tends to collect a wider variety of configurations. Keeping the acceptance ratio as the one defined for Metropolis Monte-Carlo method for global configurations (of size NxN, where N is a multiple of K), the bID stochastic process asymptotically converges to the distribution over the important energy range with a significantly wider spread than that of Boltzmann distribution estimated by Metropolis Monte Carlo technique. The proposed bID sampling method is applicable to the 2D Ising model on a larger length scale and is used to generate non-intersecting training and testing datasets of microstates. It serves as a validation tool for supervised learning algorithms and enables further exploration of various algorithmic models of the Hamiltonian operator for Ising like systems.
|