|
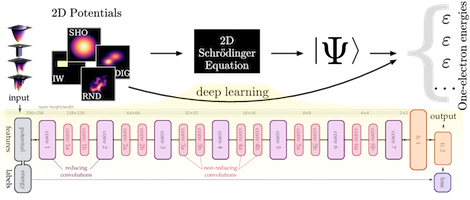
In recent years, the fields of artificial intelligence and machine learning have been advancing rapidly and convolutional neural networks (CNN) have recently gained substantial attention for their application in self-driving cars, handwriting recognition, and object classification. The use of convolutional neural networks directly and transferably to electronic structure has not, to our knowledge, ever been attempted. We numerically solved the one-electron Schr�dinger equation for millions of electrostatic potentials, and used this as training data a to train a deep convolutional neural network. We demonstrate the ability of a neural network to predict properties such as the ground-state energy, first excited state, and kinetic energy of an electron confined in four classes of two-dimensional, electrostatic potentials. The model performs extraordinarily well, predicting the ground-state energy of an electron in randomly generated potentials to a median error of 1.49 MHa, below that of chemical accuracy. Furthermore, a neural network trained on one class of potential is able to predict the energies of another class of potentials, although slightly less accurately. Overall, the exceptional performance we see suggests that convolutional neural networks could be a new approach to electronic structure theory.
|