|
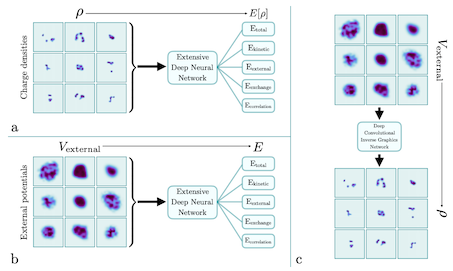
We show that deep neural networks can be integrated into, or fully replace, the Kohn-Sham density functional theory (DFT) scheme for multielectron systems in simple harmonic oscillator and random external potentials with no feature engineering. We first show that self-consistent charge densities calculated with different exchange-correlation functionals can be used as input to an extensive deep neural network to make predictions for correlation, exchange, external, kinetic, and total energies simultaneously. Additionally, we show that one can make all of the same predictions with the external potential rather than the self-consistent charge density, which allows one to circumvent the Kohn-Sham DFT scheme altogether. We then show that a self-consistent charge density found from a nonlocal exchange-correlation functional can be used to make energy predictions for a semilocal exchange-correlation functional. Lastly, we use a deep convolutional inverse graphics network to predict the charge density given an external potential for different exchange-correlation functionals and assess the viability of the predicted charge densities. This work shows that extensive deep neural networks are generalizable and transferable given the variability of the potentials (maximum total energy range
~ 100 Ha) because they require no feature engineering and because they can scale to an arbitrary system size with an
O(N) computational cost.
|