|
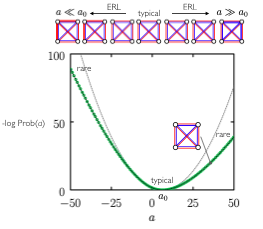
We show how to bound and calculate the likelihood of dynamical large deviations using evolutionary reinforcement learning. An agent, a stochastic model, propagates a continuous-time Monte Carlo trajectory and receives a reward conditioned upon the values of certain path-extensive quantities. Evolution produces progressively fitter agents, potentially allowing the calculation of a piece of a large-deviation rate function for a particular model and path-extensive quantity. For models with small state spaces, the evolutionary process acts directly on rates, and for models with large state spaces, the process acts on the weights of a neural network that parameterizes the model’s rates. This approach shows how path-extensive physics problems can be considered within a framework widely used in machine learning.
|