|
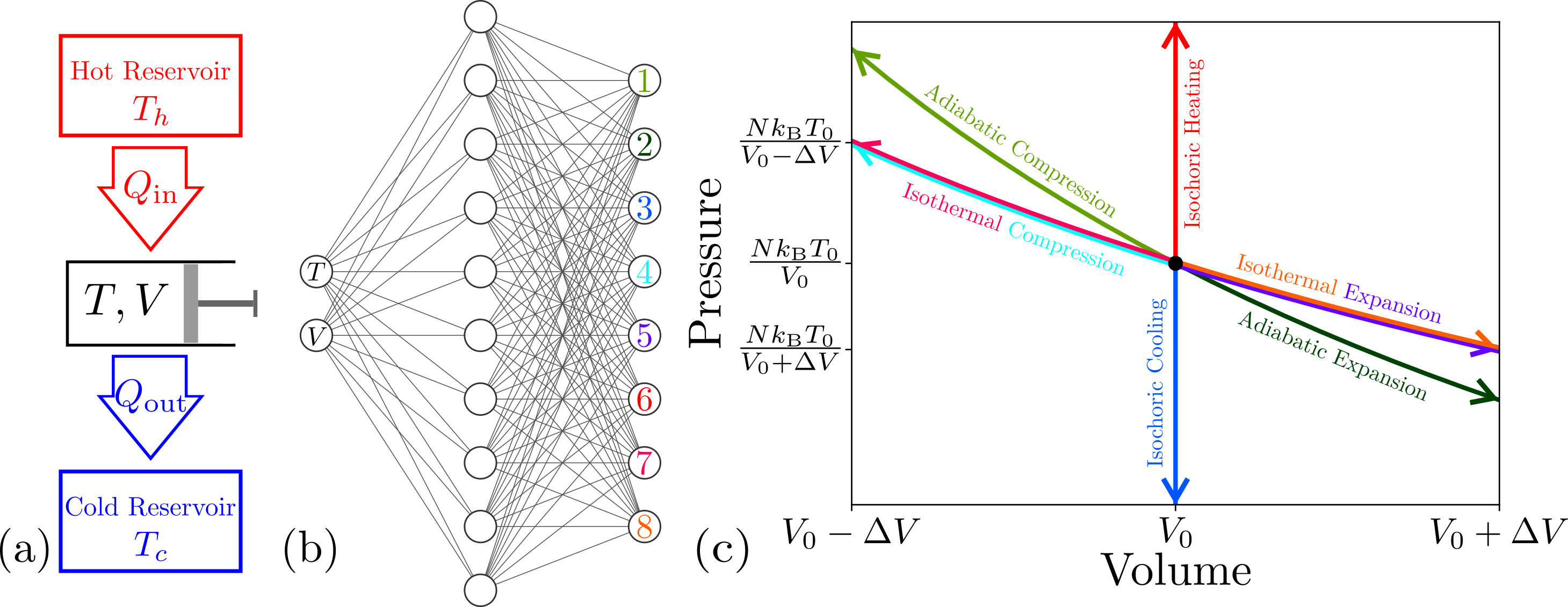
Using a model heat engine, we show that neural-network-based reinforcement learning can identify thermodynamic trajectories of maximal efficiency. We consider both gradient and gradient-free reinforcement learning. We use an evolutionary learning algorithm to evolve a population of neural networks, subject to a directive to maximize the efficiency of a trajectory composed of a set of elementary thermodynamic processes; the resulting networks learn to carry out the maximally efficient Carnot, Stirling, or Otto cycles. When given an additional irreversible process, this evolutionary scheme learns a previously unknown thermodynamic cycle. Gradient-based reinforcement learning is able to learn the Stirling cycle, whereas an evolutionary approach achieves the optimal Carnot cycle. Our results show how the reinforcement learning strategies developed for game playing can be applied to solve physical problems conditioned upon path-extensive order parameters.
|